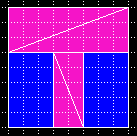
8 x 8 = 64 Quadrates
in ein
13 x 5 = 65 Rechteck.
 |
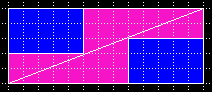
Die seltsame Verwandlung eines 8 x 8 = 64 Quadrates in ein 13 x 5 = 65 Rechteck. |
 |
| Der Ursprung des Schachbrett-Paradoxons ist zurückverfolgbar bis in das Jahr 1774, als es William Hooper in "Rational Recreations" veröffentlichte (nach David Wells: "The Penguin Book of Curious and Interesting Puzzles", 1997). | Sam Loyd senior führte das Puzzle 1858 dem Amerikanischen Schachkongress vor, 1868 erschien es in "Kurze Mitteilung" von O. Schlömilch, 1879 publizierte Schlegel die Verallgemeinerung per Fibonacci-Zahlenfolge (nach Martin Gardner: "Mathematics, Magic and Mystery", 1956). |
| Diese Version mit nur 63 Flächeneinheiten (2x(5x6)+3) stammt aus dem Buch von Henry E. Dudeney: "536 Puzzles and Curious Problems", Souvenir Press 1967. |
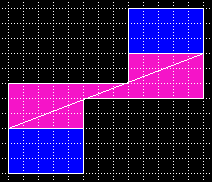 |
Das Besondere an diesen Puzzles ist die Antwort auf die Frage "Wo ist das fehlende oder entstehende Quadrat?", nämlich: "Es gibt kein fehlendes oder entstehendes Quadrat!". |
| Sägt man entsprechende Teile z. B. aus Holz zurecht, sieht alles wie bisher gezeigt aus. Aber genauer hingeschaut sehen die Teile eher so aus: | 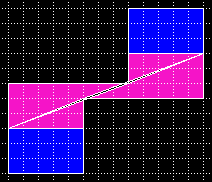 Eine überlappende Diagonale |
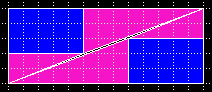 Eine Diagonale mit Lücke |
|
| Das Geheimnis besteht in einer kleinen Differenz der Winkel der Dreiecke, die einen winzigen, nahezu unsichtbaren Knick erzeugen. Die Winkeldifferenz der beiden Dreiecke 8*3 und 5*2 beträgt 0.0217 Grad. Die langgezogene Lücke hat den Flächeninhalt 1. | |
| Es gibt beliebig viele von diesen "Schachbrett"-Aufteilungen, die alle (!) mit der Fibonacci-Folge konstruierbar sind. Diese Zahlenfolge ist rekursiv definiert durch: F(0) = 0 F(1) = 1 F(n) = F(n-1) + F(n-2) |
Die beiden ersten Zahlen sind durch die Werte Null und Eins vorgegeben, jede weitere Zahl ist die Summe der beiden vorherigen. Daraus ergibt sich: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ... |
| Diese Paradoxa basieren auf der Gleichung F(n) * F(n) - F(n+1) * F(n-1) = +/-1 | ||
| 1, 1, 2, 3 | 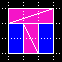 |
|
| 1, 2, 3, 5 | 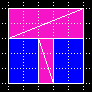 |
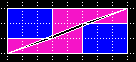 |
| 2, 3, 5, 8
(siehe oben) |
 |
 |
| 3, 5, 8, 13 | 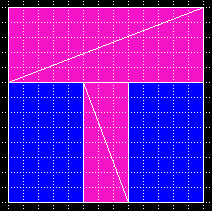 |
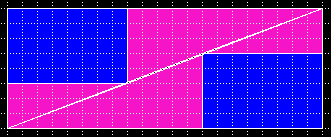 |
| 5, 8, 13, 21 | u. s. w. | |
| Es gibt zwar mehr von diesen typischen Aufteilungen eines Quadrates, aber die Teile ergeben dann kein "vollständiges" Rechteck. | ||
| Dreieck 1 | Dreieck 2 | |||
| Breite | Höhe | Breite | Höhe | |
| 3 | 1 | 2 | 1 | Fibonacci |
| 4 | 1 | 3 | 1 | |
| 5 | 1 | 4 | 1 | |
| 5 | 2 | 3 | 1 | Fibonacci |
| 5 | 3 | 2 | 1 | |
| 6 | 1 | 5 | 1 | |
| 7 | 1 | 6 | 1 | |
| 8 | 1 | 7 | 1 | |
| 8 | 3 | 5 | 2 | Fibonacci |
| 8 | 5 | 3 | 2 | |
| 9 | 1 | 8 | 1 | |
| 10 | 1 | 9 | 1 | |
| 10 | 3 | 7 | 2 | |
| 10 | 7 | 3 | 2 | |
| 11 | 1 | 10 | 1 | |
| 12 | 1 | 11 | 1 | |
| 12 | 5 | 7 | 3 | |
| 12 | 7 | 5 | 3 | |
| 13 | 1 | 12 | 1 | |
| 13 | 5 | 8 | 3 | Fibonacci |
| 13 | 8 | 5 | 3 | |
| http://mathworld.wolfram.com/DissectionFallacy.html | |
| http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibpuzzles2.html |
| Wer noch kann: mehr davon ! | |
| Dreieck ---> Dreieck | |
| Quadrat ---> Rechteck | |
| Quadrat ---> Quadrat | |
| Rechteck ---> Rechteck | |
 |
Letzte Änderung 12.9.2004 |