Dreieck --> Dreieck
Curry's-Dreieck
Curry's Paradox, Curry's Triangle, Triangle Dissection Paradox
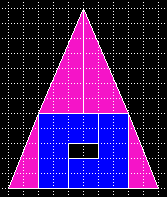
Die seltsame Verwandlung eines Dreiecks in ein gleiches, mit Loch. Dieses schöne "Paradoxon" hat Paul Curry 1953 ersonnen, ein Zauberkünstler aus New York City. Der Knick ist recht klein (0.024 Grad) und liegt nun, sehr schwer erkennbar, am Rand der geometrischen Figur.
Gardner's-Dreieck
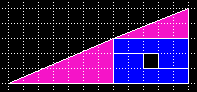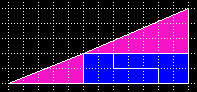
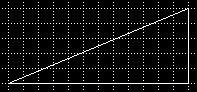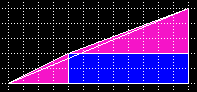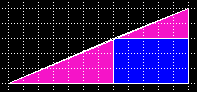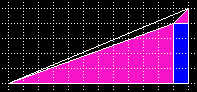
Ein halbes Curry-Dreieck hat Martin Gardner 1956 ("Mathematics, Magic and Mystery") vorgeschlagen und wurde von Roy Nauw of Kloetinge (2000) wieder entdeckt. Der Lehrer von Roy, Floor van Lamoen, veröffentlichte es in der Geometry Puzzles Newsgroup (archiviert im Math Forum)
http://mathforum.org
Noch mehr Dreiecke
Wer mag, kann wieder die Fibonacci-Folge bemühen, trifft aber dann den Kern der Sache nicht mehr. Es gibt wesentlich mehr Dreieck-Kombinationen und auch mehr als nur eine verschwundene / erzeugte Flächeneinheit. Deshalb nur kurz:
F(n) * F(n+1) - F(n-1) * F(n+2) = +/- 1
Um eine Fülle von diesen Dreiecks-Puzzles zu erzeugen, hilft eine Liste von Winkel- und Rechteckdifferenzen. So beträgt in diesem Beispiel die Flächendifferenz 2 Einheiten.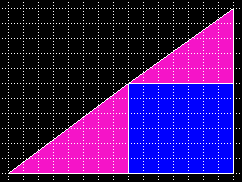
Winkeldifferenzen unter 0,03 Grad sind kaum sichtbar. Mit der folgende Tabelle ist ein Dreieck-Puzzle kaum ein Problem, bis auf die geschickte Zerlegungung der Rechteckfläche.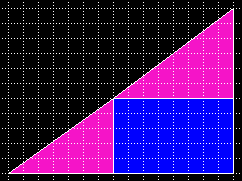
Dreieck 1 Dreieck 2 Differenzen
Breite  Höhe    Breite  Höhe    Fläche  Winkel
 6  5  5  4 +1 -0.0199973
 7  1  6  1 -1 +0.0232516
 7  3  5  2 +1 -0.0243854
 7  4  5  3 -1 +0.0212734
 7  5  4  3 -1 +0.0232516
 7  6  6  5 +1 -0.0138880
 8  1  7  1 -1 +0.0175421
 8  3  5  2 -1 +0.0217357
 8  5  3  2 -1 +0.0294033
 8  5  5  3 +1 -0.0181798
 8  5  6  4 -2 +0.0294033
 8  6  7  5 +2 -0.0232516
 8  7  6  5 +2 -0.0240917
 8  7  7  6 +1 -0.0102037
 9  1  8  1 -1 +0.0136978
 9  2  4  1 -1 +0.0263097
 9  2  5  1 +1 -0.0212734
 9  2  8  2 -2 +0.0263097
 9  4  7  3 +1 -0.0133325
 9  5  7  4 -1 +0.0120476
 9  6  8  5 +3 -0.0294033
 9  7  4  3 +1 -0.0175421
 9  7  5  4 -1 +0.0136978
 9  7  8  6 +2 -0.0175421
 9  8  7  6 +2 -0.0180161
 9  8  8  7 +1 -0.0078123
10  1  8  1 -2 +0.0246863
10  1  9  1 -1 +0.0109886
10  2  9  2 -2 +0.0212734
10  3  7  2 +1 -0.0131571
10  4  7  3 -2 +0.0243854
10  4  8  3 +2 -0.0217357
10  6  7  4 +2 -0.0212734
10  6  8  5 -2 +0.0181798
10  7  3  2 +1 -0.0227234
10  7  6  4 +2 -0.0227234
10  7  7  5 -1 +0.0095235
10  7  9  6 +3 -0.0227234
10  8  6  5 -2 +0.0199973
10  8  9  7 +2 -0.0136978
10  9  7  6 +3 -0.0241888
10  9  8  7 +2 -0.0139851
10  9  9  8 +1 -0.0061728
11  1  9  1 -2 +0.0199973
11  1 10  1 -1 +0.0090088
11  2  5  1 -1 +0.0175421
11  2  6  1 +1 -0.0147048
11  2 10  2 -2 +0.0175421
11  3  4  1 +1 -0.0212734
11  3  7  2 -1 +0.0120476
11  3  8  2 +2 -0.0212734
11  3 10  3 -3 +0.0252047
11  4  3  1 +1 -0.0270204
11  4  6  2 +2 -0.0270204
11  4  8  3 -1 +0.0099997
11  4  9  3 +3 -0.0270204
11  5  7  3 +2 -0.0217357
11  5  9  4 +1 -0.0084032
11  6  7  4 -2 +0.0197994
11  6  9  5 -1 +0.0077518
11  7  3  2 -1 +0.0212734
11  7  5  3 +2 -0.0263097
11  7  6  4 -2 +0.0212734
11  7  8  5 +1 -0.0081299
11  7  9  6 -3 +0.0212734
11  7 10  6 +4 -0.0263097
11  8  4  3 -1 +0.0147048
11  8  7  5 +1 -0.0085468
11  8  8  6 -2 +0.0147048
11  8 10  7 +3 -0.0180703
11  9  5  4 +1 -0.0109886
11  9  6  5 -1 +0.0090088
11  9  7  6 -3 +0.0228968
11  9  9  7 +4 -0.0246863
11  9 10  8 +2 -0.0109886
11 10  7  6 +4 -0.0291888
11 10  8  7 +3 -0.0189851
11 10  9  8 +2 -0.0111727
11 10 10  9 +1 -0.0050000
12  1  9  1 -3 +0.0275160
12  1 10  1 -2 +0.0165274
12  1 11  1 -1 +0.0075187
12  2  7  1 +2 -0.0232516
12  2 11  2 -2 +0.0147048
12  3  9  2 +3 -0.0263097
12  3 11  3 -3 +0.0212734
12  4 11  4 -4 +0.0270204
12  5  5  2 +1 -0.0142847
12  5  7  3 -1 +0.0101007
12  5  9  4 -3 +0.0234332
12  5 10  4 +2 -0.0142847
12  7  5  3 -1 +0.0123451
12  7  7  4 +1 -0.0089283
12  7  9  5 +3 -0.0209759
12  7 10  6 -2 +0.0123451
12  7 11  6 +5 -0.0287277
12  8  8  5 +4 -0.0294033
12  8 10  7 -4 +0.0227234
12  8 11  7 +4 -0.0212734
12  9  7  5 +3 -0.0232516
12  9  9  7 -3 +0.0175421
12  9 11  8 +3 -0.0147048
12 10  5  4 +2 -0.0199973
12 10  7  6 -2 +0.0138880
12 10  8  7 -4 +0.0240917
12 10 10  8 +4 -0.0199973
12 10 11  9 +2 -0.0090088
12 11  8  7 +4 -0.0231173
12 11  9  8 +3 -0.0153049
12 11 10  9 +2 -0.0091322
12 11 11 10 +1 -0.0041322
13  1 10  1 -3 +0.0228968
13  1 11  1 -2 +0.0138880
13  1 12  1 -1 +0.0063693
13  2  6  1 -1 +0.0124993
13  2  7  1 +1 -0.0107523
13  2  8  1 +3 -0.0282943
13  2 11  2 -4 +0.0272042
13  2 12  2 -2 +0.0124993
13  3  4  1 -1 +0.0181798
13  3  5  1 +2 -0.0294033
13  3  8  2 -2 +0.0181798
13  3  9  2 +1 -0.0081299
13  3 10  2 +4 -0.0294033
13  3 12  3 -3 +0.0181798
13  4  3  1 -1 +0.0232516
13  4  6  2 -2 +0.0232516
13  4  7  2 +2 -0.0201993
13  4  9  3 -3 +0.0232516
13  4 10  3 +1 -0.0070421
13  4 12  4 -4 +0.0232516
13  5  5  2 -1 +0.0133325
13  5  8  3 +1 -0.0084032
13  5 10  4 -2 +0.0133325
13  5 11  4 +3 -0.0184028
13  5 12  5 -5 +0.0276173
13  6  7  3 +3 -0.0275160
13  6  9  4 +2 -0.0141834
13  6 11  5 +1 -0.0057803
13  7  7  4 -3 +0.0252047
13  7  9  5 -2 +0.0131571
13  7 11  6 -1 +0.0054054
13  8  5  3 +1 -0.0112355
13  8  8  5 -1 +0.0069443
13  8 10  6 +2 -0.0112355
13  8 11  7 -3 +0.0150742
13  8 12  7 +5 -0.0235805
13  9  3  2 +1 -0.0175421
13  9  6  4 +2 -0.0175421
13  9  7  5 -2 +0.0147048
13  9  9  6 +3 -0.0175421
13  9 10  7 -1 +0.0051813
13  9 11  8 -5 +0.0232516
13  9 12  8 +4 -0.0175421
13 10  4  3 +1 -0.0121945
13 10  5  4 -2 +0.0190453
13 10  8  6 +2 -0.0121945
13 10  9  7 -1 +0.0053475
13 10 10  8 -4 +0.0190453
13 10 11  8 +6 -0.0268993
13 10 12  9 +3 -0.0121945
13 11  5  4 +3 -0.0275160
13 11  6  5 +1 -0.0075187
13 11  7  6 -1 +0.0063693
13 11  8  7 -3 +0.0165731
13 11  9  8 -5 +0.0243854
13 11 10  8 +6 -0.0275160
13 11 11  9 +4 -0.0165274
13 11 12 10 +2 -0.0075187
13 12  8  7 +5 -0.0265895
13 12  9  8 +4 -0.0187771
13 12 10  9 +3 -0.0126044
13 12 11 10 +2 -0.0076044
13 12 12 11 +1 -0.0034722

http://www.mathematik.uni-bielefeld.de/%7Esillke/PUZZLES/jigsaw-paradox.html
Zurück Letzte Änderung 12.9.2004