Siehe auch: Sagnac M. G., J. de Phys., 1914, 4, 177-195

| "L'éther lumineux démontré par l'effet du vent relatif d'éther dans un interféromêtre en rotation uniforme." und "Sur la preuve de la réalité de l'éther lumineux par l'éxperience de l'interférographe tournant.", Comptes Rendus 157. Siehe auch: Sagnac M. G., J. de Phys., 1914, 4, 177-195 |
 |
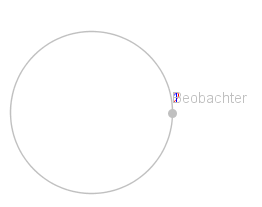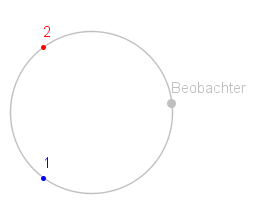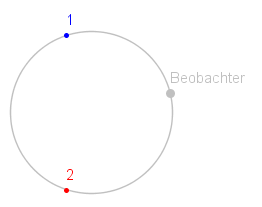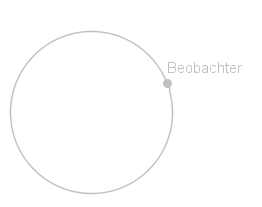
| Georges Sagnac konstruierte ein Interferometer auf einer Drehscheibe. Ein kohärenter Lichtstrahl wird per Strahlteiler über ein Spiegelsystem gegenläufig einmal herum "im Kreis" geführt. Die Lichtquelle und der Beobachter befinden sich ebenfalls auf der Drehscheibe. Dreht sich die Apparatur, tritt eine Phasenverschiebung des Lichtes auf (Sagnac-Effekt), je nach Drehrichtung und Drehgeschwindigkeit. Sagnac deutete diese Beobachtung als Nachweis der Existenz des Lichtäthers. | Der Sagnac-Effekt ist bei beliebigen, vieleckigen Lichtwegen zu beobachten und funktioniert auch ohne Spiegel mit einem kreisförmigen Lichtweg (Faserkreisel, Laserkreisel). |
| Das Licht in Rotationsrichtung muss einen längeren Weg zurücklegen, da sich während der Laufzeit auch der Beobachter weiterbewegt hat. Das entgegen der Rotationsrichtung umlaufende Licht hat einen kürzeren Weg. Die Differenz der Laufzeiten ist als Phasenverschiebung zu beobachten. |
 |
| Völlig unrelativistisch erhält man mit t = Zeit B = Geschwindigkeit des Beobachters L = Geschwindigkeit des Lichts U = Umlaufstrecke und für die Orte o des Betrachtes (oB) bzw. der Lichtsignale oB(t) = B * t oL1(t) = -U + L * t oL2(t) = +U - L * t die beiden Zeiten des Eintreffens t1 = U / ( L - B ) t2 = U / ( L + B ) und schließlich: delta t = 2*U*B / (L2-B2) |
Die klassische Interpretation versteht den Sagnac-Effekt als verschieden lange Laufwege, die einen Laufzeitunterschied ergeben. Für das Bezugssystem des Beobachters ist die Lichtgeschwindigkeit der beiden Signale verschieden. Dies steht im Widerspruch zu den beiden Relativitätstheorien. Die spezielle Relativitätstheorie versagt hier scheinbar, weil rotierende (also beschleunigte) Bezugssysteme nicht vorgesehen sind. Aber der Kreis kann aufgebogen werden und ergibt ein lineares Sagnac-Interferometer. Es funktioniert genauso, mit konstanter Geschwindigkeit und ohne beschleunigte Bewegung. In der Speziellen Relativitätstheorie ist die lineare Sagnac-Anordnung beschrieben, mit der seltsamen Schlussfolgerung der relativen Gleichzeitigkeit. In der Allgemeinen Relativitätstheorie (1916) ist die kreisförmige Sagnac-Anordnung beschrieben, allerdings ohne Bezugnahme auf Sagnac und ebenfalls mit recht seltsamen Schlussfolgerungen: Einheitsmaßstäbe und Normaluhren sind unbrauchbar (siehe weiter unten). |
 |
 |
| Rechnet man das Interferometer mit Huygens-Wellen durch, hat auf ein ruhendes Sagnac-Interferometer ein evtl. wehender Ätherwind kaum Einfluss auf die Phase der beobachteten Wellenfronten. | Der stärkste Effekt besteht in der Ablenkung der Wellenfronten. Dies aber nur bei galaktischen Ausmaßen der Apparatur. |
| 1925 gelang es mit einem Sagnac-Interferometer von 613 m Länge und 339 m Breite die Rotation der Erde mit einer relativen Genauigkeit von 2% zu messen. A. A. Michelson, Henry G. Gale, F. Pearson: "The Effect of the Earth's Rotation on the Velocity of Light", Astrophysical Journal 61, 1925. |
137 138 139 140 141 142 143 144 145 |
| Im Lauf der Jahrzehnte wurden etliche Variationen dieses Interferometers gebaut: Lichtwege im Vakuum oder in allerlei Gasen und Gläsern. Mit stationären Spiegeln und rotierenden Medien; mit stationärer Lichtquelle und stationärem Beobachter, während die Spiegel auf der Drehscheibe rotieren (Dufour und Prunier). |
Die Ergebnisse stimmten immer mit denen von Sagnac überein. |
| Die Verrenkungen von Einstein, um sein 2. Postulat von der Konstanz der Lichtgeschwindigleit zu retten: |
| Einstein 1916: Die Grundlage der allgemeinen Relativitätstheorie §3. Das Raum-Zeit-Kontinuum. Forderung der allgemeinen Kovarianz für die die allgemeinen Naturgesetze ausdrückenden Gleichungen. "... Wir führen in einem Raume, der frei sei von Gravitationsfeldern, ein Galileisches Bezugssystem K(x,y,z,t) ein, und außerdem ein relativ zu K gleichförmig rotierendes Koordinatensystem K' (x', y', z' t'). Die Anfangspunkte beider Systeme sowie deren Z-Achsen mögen dauernd zusammenfallen. Wir wollen zeigen, daß für eine Raum-Zeitmessung im System K' die obige Festsetzung für die physikalische Bedeutung von Längen und Zeiten nicht aufrecht erhalten werden kann. Aus Symmetriegründen ist klar, daß ein Kreis um den Anfangspunkt in der X-Y-Ebene von K zugleich als Kreis in der X'-Y'-Ebene von K' aufgefaßt werden kann. Wir denken uns nun Umfang und Durchmesser dieses Kreises mit einem (relativ zum Radius unendlich kleinen) Einheitsmaßstabe ausgemessen und den Quotienten beider Meßresultate gebildet. Würde man dieses Experiment mit einem relativ zum Galileischen System K ruhenden Maßstabe ausführen, so würde man als Quotienten die Zahl pi erhalten. Das Resultat der mit einem relativ zu K' ruhenden Maßstabe ausgeführten. Bestimmung würde eine Zahl sein, die größer ist als pi. Man erkennt dies leicht, wenn man den ganzen Meßprozeß vom "ruhenden" System K aus beurteilt und berücksichtigt, daß der peripherisch angelegte Maßstab eine Lorentzverkürzung erleidet, der radial angelegte Maßstab aber nicht. Es gilt daher in bezug auf K' nicht die Euklidische Geometrie; der oben festgelegte Koordinatenbegriff, welcher die Gültigkeit der Euklidischen Geometrie voraussetzt, versagt also mit Bezug auf das System K'. Ebensowenig kann man in K' eine den physikalischen Bedürfnissen entsprechende Zeit einführen, welche durch relativ zu K' ruhende, gleich beschaffene Uhren angezeigt wird. Um dies einzusehen, denke man sich im Koordinatenursprung und an der Peripherie des Kreises je eine von zwei gleich beschaffenen Uhren angeordnet und vom "ruhenden" System K aus betrachtet. Nach einem bekannten Resultat der speziellen Relativitätstheorie geht - von K aus beurteilt - die auf der Kreisperipherie angeordnete Uhr langsamer als die im Anfangspunkt angeordnete Uhr, weil erstere Uhr bewegt ist, letztere aber nicht. Ein im gemeinsamen Koordinatenursprung befindlicher Beobachter, welcher, auch die an der Peripherie befindliche Uhr mittels des Lichtes zu beobachten fähig wäre, würde also die an der Peripherie angeordnete Uhr langsamer gehen sehen als die neben ihm angeordnete Uhr. Da er sich nicht dazu entschließen wird, die Lichtgeschwindigkeit auf dem in Betracht kommenden Wege explizite von der Zeit abhängen zu lassen, wird er seine Beobachtung dahin interpretieren, daß die Uhr an der Peripherie "wirklich" langsamer gehe als die im Ursprung angeordnete. Er wird also nicht umhin können, die Zeit so zu definieren, daß die Ganggeschwindigkeit einer Uhr vom Orte abhängt. Wir gelangen also zu dem Ergebnis: In der allgemeinen Relativitätstheorie können Raum- und Zeitgrößen nicht so definiert werden, daß räumliche Koordinatendifferenzen unmittelbar mit dem Einheitsmaßstab, zeitliche mit einer Normaluhr gemessen werden könnten. ..." |
Einstein 1917: Über die spezielle und die allgemeine Relativitätstheorie § 23 Verhalten von Uhren und Maßstäben auf einem rotierenden Bezugskörper. "... Wir gehen wieder von oft herangezogenen, ganz speziellen Fällen aus. Es liege ein raum-zeitliches Gebiet vor, in welchem relativ zu einem Bezugskörper K von passend gewähltem Bewegungszustande kein Gravitationsfeld existiere; in bezug auf das ins Auge gefaßte Gebiet ist dann K ein GALILEIscher Bezugskörper, und es gelten relativ zu K die Ergebnisse der speziellen Relativitätstheorie. Dasselbe Gebiet denken wir uns auf einem zweiten Bezugskörper K´ bezogen, welcher relativ zu K gleichförmig rotiert. Um die Vorstellung zu fixieren, denken wir uns K´ in Gestalt einer ebenen Kreisscheibe, welche um ihren Mittelpunkt in ihrer Ebene gleichmäßig rotiere. Ein exzentrisch auf der Kreisscheibe K´ sitzender Beobachter empfindet eine Kraft, die in radialer Richtung nach außen wirkt, und welche von einem relativ zum ursprünglichen Bezugskörper K ruhenden Beobachter als Trägheitswirkung (Zentrifugalkraft) gedeutet wird. Der auf der Scheibe sitzende Beobachter möge jedoch seine Scheibe als "ruhenden" Bezugskörper auffassen; dazu ist er auf Grund des allgemeinen Relativitätsprinzips berechtigt. Die auf ihn und überhaupt auf relativ zur Scheibe ruhende Körper wirkende Kraft faßt er als Wirkung eines Gravitationsfeldes auf. ... Der Beobachter stelle zunächst von zwei gleich beschaffenen Uhren die eine in dem Mittelpunkte der Kreisscheibe, die andere an der Peripherie derselben auf, so daß sie relativ zur Kreisscheibe ruhen. Wir fragen uns zunächst, ob diese beiden Uhren gleich schnell gehen vom Standpunkt des nicht rotierenden GALILEIschen Bezugskörpers K. Von diesem aus beurteilt, hat die Uhr im Mittelpunkt keine Geschwindigkeit, während die Uhr an der Peripherie infolge der Rotation relativ zu K in Bewegung ist. Nach einem Ergebnis des § 12 geht deshalb die letztere Uhr von K aus beurteilt dauernd langsamer als die Uhr in der Mitte der Kreisscheibe. Dasselbe müßte offenbar auch der Mann auf der Kreisscheibe konstatieren, den wir uns etwa als in der Mitte der Kreisscheibe neben der dortigen Uhr sitzend vorstellen wollen. Auf unserer Kreisscheibe und allgemeiner in jedem Gravitationsfelde wird also eine Uhr rascher oder langsamer laufen, je nach der Stelle, in welcher die Uhr (ruhend) angeordnet ist. Eine vernünftige Definition der Zeit mit Hilfe von relativ zum Bezugskörper ruhend angeordneten Uhren ist also nicht möglich. Eine ähnliche Schwierigkeit zeigt sich, wenn man versucht, unsere frühere Definition der Gleichzeitigkeit hier anzuwenden, worauf ich nicht weiter eingehen will. Aber auch die Definition der räumlichen Koordinaten macht hier zunächst unüberwindliche Schwierigkeiten. Legt nämlich der mit der Scheibe bewegte Beobachter seinen Einheitsmaßstab (ein relativ zum Scheibenradius kleines Stäbchen) an der Scheibenperipherie tangential zu dieser an, so ist derselbe, vom GALILEIschen System aus beurteilt, kürzer als 1, weil bewegte Körper nach § 12 in Richtung der Bewegung eine Verkürzung erfahren. Legt er dagegen seinen Maßstab in die Richtung des Scheibenradius, so erfährt dieser, von K aus beurteilt, keine Verkürzung. Mißt der Beobachter also zuerst den Scheibenumfang, dann den Scheibendurchmesser mit seinem Maßstab und dividiert er hierauf diese beiden Meßergebnisse, so findet er als Quotienten nicht die bekannte Zahl pi = 3,14..., sondern eine größere Zahl, während sich auf einer relativ zu K ruhenden Scheibe bei dieser Operation natürlich exakt pi ergeben müßte. Damit ist bereits bewiesen, daß die Sätze der euklidischen Geometrie auf der rotierenden Scheibe und damit überhaupt in einem Gravitationsfelde nicht genau gelten können, wenigstens wenn man dem Stäbchen überall und in jeder Orientierung die Länge 1 zuschreibt. ..." |
| Eine Erklärung des Sagnac-Effekts per Allgemeiner Relativitätstheorie steht noch aus. |
 |
Letzte Änderung 14.2.2006 |