
 |
Eine Mini-Jakobsleiter mit nur zwei Blöcken ist wie ein Buch, dass auf beiden Seiten aufgeschlagen werden kann und dennoch zusammen hält. Sind die beiden Bänder am Rand recht schmal und dasjenige in der Mitte möglichst breit, erhält man ein "Büchlein" mit zwei verschiedenen Inhalten. |
| Aus einem Blatt kariertem (oder doppelt geknifftem) Papier ist rasch die folgende Form ausgeschnitten. Man sieht die ersten Seiten des Büchleins und eine Umschlagseite: | |
 |
|
| An der gestrichelten Linie wird dann das Papier nach hinten umgeknickt und die Lasche durch die Öffnung nach vorn gezogen. Die zweiten Seiten werden sichtbar und es entsteht dann so etwas: | |
 |
Klebt man nun die Lasche am rechten Rand mit einem möglichst unsichtbaren Klebestreifen (das dunkelgraue Rechteck) an, und faltet das Ganze an der gestrichelten Linie nach vorn zusammen, ist das Jakobsbuch fertig. Wer mag, kann die Beschriftung (wie angedeutet) übernehmen: eine Geschichte, die sich ewig wiederholt. |
| Dieser Falter ist eine sehr einfache Form eines Tri-Tetraflexagons und funktioniert auch mit nur zwei "Bändern". | 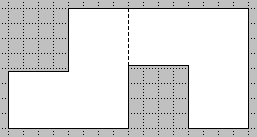 |
| Bastelbögen: | Der rekursive Doppelmops Tri-Tetraflexagon-Buch-Muster |
| Flexagone sind gefaltete Papierblätter, die in gewisser Weise umgeblättert, umgestülpt, umgekrempelt werden können und dann verschiedene Oberflächen zeigen. Das Jakobsbuch ist ein Tetraflexagon, also ein 4-eckiges Objekt. Je nach Anzahl der Oberflächen gibt es Tri-Tetraflexagone, Tetra-Tetraflexagone usw. | Die mir bekannten Tetraflexagone sind nicht endlos krempelbar und müssen "am Ende" umgedreht werden. Berühmter sind die Hexaflexagone (also 6-eckige Objekte), die ein endloses krempeln erlauben. |
| Ein Tetraflexagon mit 4 Ansichten, also ein Tetra-Tetraflexagon, kann wie ein Jakobsbuch endlos "durchblättert" werden, hat allerdings eine verborgene (4.) Seite. Einfacher ist, eine Art Bilderbuch daraus herzustellen: es bieten sich die 4 Jahreszeiten, die 4 Sätze einer Symphonie oder die 4 Musketiere (ähemm) an. Oder völlig verdrehbar: 4 Gesichter, die sich durch "auf den Kopf stellen" auf den Kopf stellen. | |
 |
 |
 |
 |
| 4-4-Flexagon | http://www.artistbooks.com/editions/flexintro.html http://www.mathnstuff.com/papers/tetra/tetra.htm http://cs.bmcc.cc.or.us/mth213/Labs/tetraflexagon%20lab.htm |
|
| x-4-Flexagone | http://mathworld.wolfram.com/Tetraflexagon.html | |
| Pop-Up Karten | keine Flexagone | http://marivi_10.tripod.com |
| Letzte Änderung 29.8.2005 |