
| Sind 2 gleiche Fadenpendel locker miteinander verbunden, können sie sich gegenseitig beeinflussen (ist das eine Tautologie?). Sie haben dann die seltsame Eigenschaft, dass irgendwann nur das eine pendelt, während das andere ruht, um dann wieder miteinander zu pendeln, bis irgendwann das eine ruht und das andere pendelt. Der Anblick ist verblüffend. Es gibt eine Fülle von Kopplungsmechanismen. Hier ein paar Beispiele: |
||
 |
 |
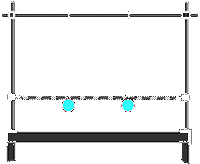 |
| Im einfachsten Fall sorgt ein Faden zwischen den Pendeln für die Kopplung. | Ein starrer Stab. | Kopplung per Spiralfedern. |
 |
 |
|
| Alles hängt an Spiralfedern. | ||
Torsionswellenapparat nach Julius  |
||
| 2-3 identische Fadenpendel an einem flexiblen Metallrahmen tauschen Energie aus. | Wäscheklammern an einem gespannten Gummifaden in gleichmäßigen Abständen angeklammert zeigen in einfacher Weise die Ausbreitung einer "Welle". | |
Hier ist ein reales gekoppeltes Pendel zu sehen. Zwei Stahlkugeln, an Ketten befestigt und über eine weitere Kette gekoppelt, schwingen bis zu 15 Minuten. Die sichtbare "Ruhezeit" eines Pendels beträgt bis zu 3 Sekunden. Ein perfektes Gerät. Die Halterung besteht aus einem stabilen Holzrahmen, der möglichst nicht mitschwingen darf. |
 |
| Eine optimale Bewegung ist nur mit langwierigem Herumprobieren und Verstellen an den Aufhängungen der Pendel und der koppelnden Kette zu erreichen. Ketten sind deshalb praktisch, weil das Justieren durch einfaches Einhaken in die Kettenglieder erfolgen kann und ein Verrutschen ausgeschlossen ist. Die Konstruktion lädt zum weiteren Experimentieren ein. So können schnell die Gewichte ausgetauscht oder unterschiedliche Pendellängen eingestellt werden. |
|
Zwar nicht gekoppelt, aber schön anzuschauen ist eine Reihe von Fadenpendeln mit verschiedenen Frequenzen. Lenkt man sie gleichzeitig aus, zeigen sich Wellenmuster.  |
Eine Spiralfeder kann wie ein Fadenpendel hin- und her- (transversal), aber typischerweise auch auf- und abschwingen (longitudinal). Als dritte Schwingungsart gibt es die Drehschwingung (torsional). Alle diese Schwingungen sind bereits automatisch miteinander gekoppelt, so dass eine Spiralfeder zu sehr kurzweiligen Bewegungen neigt.  |
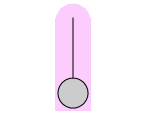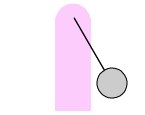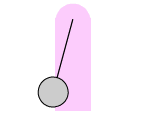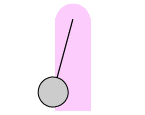
| Eine eindrucksvolle Demonstration von abwechselnden longitudinalen und torsionalen Schwingungen zeigt das Wilberforce-Pendel, benannt nach dem englischen Physiker Lionel Robert Wilberforce (1861-1944). Setzt man das Pendel durch Ziehen in Bewegung, schwingt es zuerst auf und ab. Nach kurzer Zeit beginnt das Gewicht - weiter auf und ab schwingend - sich um die eigene Achse zu drehen (wie beim Torsionspendel). Diese Bewegung herrscht immer mehr vor, bis sich die Masse schließlich nur noch dreht, ohne zu pendeln. Danach kehrt sich der Vorgang um. Es tritt wieder eine stärkere Auf- und Abbewegung auf. |  |
Genaueres Das Wilberforce-Pendel ist eine Schraubenfeder, wobei die longitudinale und die torsionale Resonanzfrequenz identisch ist. Bei der Auf- und Ab-Bewegung ergibt sich diese Frequenz aus dem Zusammenwirken der Federkonstanten und der angehängten Masse. Bei der Drehschwingung spielt die Trägheitskonstante des angehängten Körpers eine Rolle. Dehnt man die Feder, wird gleichzeitig eine kleine Drehbewegung hervorgerufen, die die Drehschwingung anregt. Umgekehrt ruft eine Verdrehung der Feder eine kleine Längenänderung hervor, die wiederum die Längsschwingung anregt. Energie fließt per Resonanz so lange in eine Richtung, bis die jeweilige 'kleine' Bewegung erreicht ist.
 Ein Wilberforce-Pendel aus der Hand von Jochen Valett. |
|
| Weniger elegant, aber genauso bemerkenswert wie das Wilberforce-Pendel, ist die Resonanz longitudinal / transversal. Auf diese Art und Weise können wir auf einer Schaukel sitzend immer höher und höher schaukeln (entsprechende Bewegungen vorausgesetzt, d. h. Schwerpunktverlagerungen). |
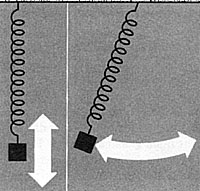 |
| Schlichting, Hans-Joachim; Ucke, Christian Das "Metapendel" oder: eine sich selbst antreibende Schaukel Physik in unserer Zeit 26 (1995), Heft 1, 41-42 |
 |
Letzte Änderung 14.10.2002 |